Game

Memory limit: 32 MB

Let us consider a game on a rectangular board 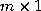consisting of 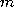elementary squares numbered successively from 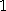to 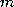. There are pawns on the board, each on a distinct square. None of them occupies the square with number 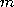. Each single move in the is the following action: the moving player picks a pawn from any occupied square chosen at will and places it on the first unoccupied square with a larger number. The two players make moves in turn. The one who puts a pawn on the last square, i.e. the square with a number 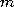, wins.

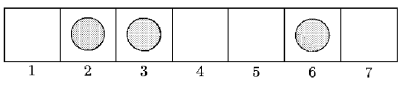
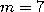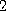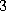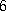In the case presented in the figure (), a player is allowed to move a pawn from square no. to , from square no. to or from square no. to 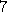. The latter ends the game.

We say a player's move is winning if after making it he can win the game, no matter what moves his opponent makes.

Task

Write a programme that:

• reads the size of a board and the initial setup of pawns from the standard input,
• determines the number of distinct winning moves the starting player may choose in the given initial situation,
• writes the result to the standard output.

Input

The first line of the input contains two integers 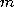and (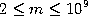, , 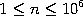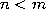) separated by a single space. The second line contains increasing numbers - these are the numbers of squares the pawns are set on. Numbers in the line are separated by single spaces.

Output

The first and only output line should contain the number of distinct winning moves possible for the starting player in the given initial situation.

Example

For the input data:

5 2
1 3

the correct result is:

1

and for the following input data:

5 2
2 3

the correct answer is:

0

Task author: Bartosz Walczak.